Effort and Error

The effort expended in speech, G (Equation 1), can be approximated from knowledge about muscle dynamics [16]. Qualitatively, our effort term behaves like the physiological effort: it is zero if muscles are stationary in a neutral position, and increases as motions become faster and stronger. Minimizing G tends to make the pitch curve smooth and continuous, because it minimizes the magnitude of the first and second derivatives of the pitch.

The error term, R (Equations 2 and 3), behaves like a communications error rate: it is zero if the prosody exactly matches an ideal tone template, and it increases as the prosody deviates from the template. The choice of template encodes the lexical information carried by the tones. The speaker tries to minimize the deviation, because if it becomes too large, the speaker will expect the listener to mis-classify the tone and possibly misinterpret the utterance.

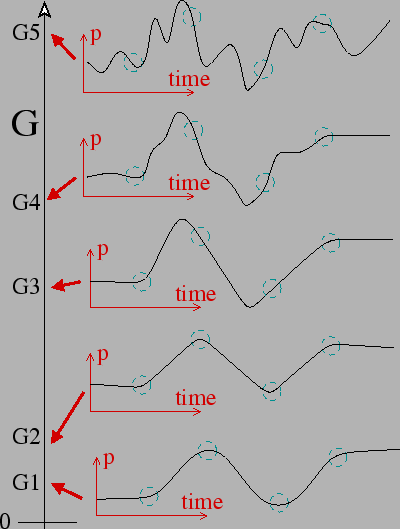
Figure 1 shows how the G (effort) term depends on the shape of e. The curves we show all go through the same set of pitch targets (dashed circles). The G values increase with the RMS curvature and slope of e. In this case, optimal pitch curve has the smallest value of G, G₁.

Figure 1: Schematic showing the dependence of G on the shape of the pitch curve. The large, left axis shows values of G (speech effort) for each of the displayed curves (G₁ ...G₅). Each small axes show sample curves of pitch as a function of time. The resulting Stem-ML pitch curve is the one with the optimal (smallest) value of G + R. Because we have chosen R = 0 in this example, the solution here is G₁, the one with the smallest G.