In Stem-ML, a ``tag'' is a tone template, along with a few
parameters that describe the scope of the template and how the
template interacts with its environment. It corresponds to the
mathematical description of an intonation event (e.g., a
tone or an accent). Variables in the equations below are defined in
Table 2.2.3. Tags have
a parameter, type, which controls whether errors in the
shape or average value of the pitch curve are most important. In
this work, the targets, y, consist of an tone component riding on
top of the phrase curve, p.
In order to efficiently solve the optimization problem, and
calculate the surface realization of prosody, we write simple
approximations to G and
R so that the model can be solved
efficiently as a set of linear equations:
G = 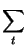 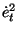 + ( + (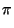 . smooth/2)2
. smooth/2)2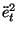 + adroop2 .
et2 + adroop2 .
et2 |
(1) |
R =  sk2rk sk2rk |
(2) |
rk =
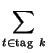 cos(type
. cos(type
. 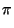 /2)(et -
yk, t)2 + sin(type . /2)(et -
yk, t)2 + sin(type .
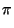 /2)( /2)(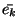 - - 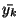 )2, )2, |
(3) |
where
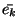 = = 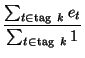 ,
, |
(4) |
and
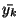 = = 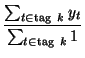 .
. |
(5) |
and
Finally, f0 is
e, scaled to the speaker's pitch
range:
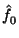 = g(e, = g(e,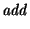 ) . range +
base ) . range +
base |
(6) |
so that p and e are dimensionless quantities, typically
between 0 and 1. The function g()
handles linear (add = 1) or
Fujisaki (add = 0) scaling:
g(e, 1) = e for any
e, and also
g(0,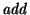 ) = 0
and
g(1,
) = 0
and
g(1,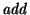 ) = 1
for any add.
) = 1
for any add.
Table: Definitions of parameters and
variables used in this paper. Daggers denote parameters defined
more fully in [8].
| Symbol |
Location |
Meaning |
add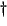 |
Eq. 6 |
Controls the mapping between e and f0. See g(). |
adroop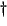 |
Eq. 1 |
Rate at which e
droops toward the phrase curve in the absence of a tag. |
base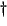 |
Eq. 6 |
The speaker's relaxed f0. |
smooth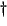 |
Eq. 1 |
Response time of muscles. |
type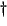 |
Eq. 3 |
Is tone defined by its shape (0) or f0 value (1). |
| atype |
Eq. 7 |
Controls how the amplitude of the template depends
on the strength of a word. |
| f0 |
many places |
Measured pitch. |
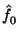 |
Eq. 6 |
Modeled pitch. |
e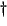 ,
et ,
et |
§2.2.3 |
Emphasis, i.e., 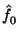 relative to the
speaker's range. relative to the
speaker's range. |
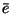 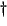 |
Eqs. 3, 4 |
Mean emphasis over the scope of a tag. |
y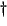 ,
yt ,
yt |
§2.2.3 |
Tone template. |
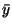  |
Eqs. 3, 5 |
Mean value of a tone template. |
G |
Eq. 1 |
Effort expended in realizing the pitch
contour. |
| ri |
Eq. 3 |
The summed error for word i between the template and the realized
pitch. |
R |
Eq. 2 |
The summed error for an utterance between the
ideal templates and the realized pitch contour. |
g()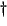 |
Eq. 6 |
Function to map between subjective emphasis
(e) and objective f0. |
|
Greg Kochanski, Chilin Shih 2002-08-03