Classifier architecture and Features.1
Greg Kochanski
http://kochanski.org/gpk
February 14, 2004
To talk about ``close'' and ``far'' in a consistent
manner, we need to have the concept of a distance
metric.
A distance metric, 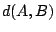 is a function or algorithm
for calculating a distance between two things,
is a function or algorithm
for calculating a distance between two things, 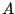 and
and 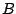 .
It has three properties:
.
It has three properties:
- It is always positive or zero.
- The distance from a thing2 to itself is zero.
- It obeys the triangle inequality:
For any three points,
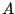 ,
, 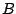 , and
, and 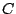 ,
,
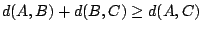 for any possible choice of
for any possible choice of 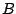 .
In other words, the straight line between
.
In other words, the straight line between
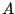 and
and 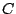 , which has a length
, which has a length 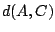 ,
is shorter3 than any other path between
,
is shorter3 than any other path between 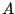 and
and 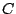 , such as a path that goes by
way of
, such as a path that goes by
way of 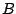 .
.
Anything that obeys these three properties is a distance
metric.
Common examples are Euclidean distance in two
dimensions:
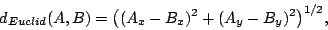 |
(1) |
and city block metric [#!cityblock!#]:
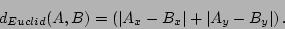 |
(2) |
(The Euclidean and city-block metrics generalize to any
number of dimensions in a straightforward manner.)
Greg Kochanski
2004-02-14
![]() is a function or algorithm
for calculating a distance between two things,
is a function or algorithm
for calculating a distance between two things, ![]() and
and ![]() .
It has three properties:
.
It has three properties: